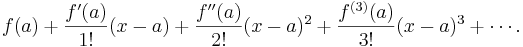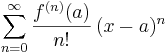Difference between revisions of "Taylor Series"
From Sean_Carver
(→New Concept: Taylor Series) |
(→New Concept: Taylor Series) |
||
| Line 26: | Line 26: | ||
:<math> \sum_{n=0} ^ {\infin } \frac {f^{(n)}(a)}{n!} \, (x-a)^{n}</math> | :<math> \sum_{n=0} ^ {\infin } \frac {f^{(n)}(a)}{n!} \, (x-a)^{n}</math> | ||
| + | |||
| + | * '''Convergence:''' A function whose Taylor series converges to the function is called ''analytic''. But sometimes, as we have seen with power series generally, convergence can be local (i.e. only in some interval). | ||
Revision as of 21:59, 14 March 2011
Review Concepts
- Sequences
- Convergence
- Infinite series
- The sequence of partial sums of an infinite series
- Power series
New Concept: Taylor Series
- Think of Taylor series as a special kind of power series, where the sequence of partial sums are meant as better and better approximations of some other function.
- The Taylor Series is derived from the function.
Definition copied, verified, and adapted from Wikipedia, this page (permanent link). See license to copy, modify, distribute.
The Taylor series of a function ƒ(x) at a is the power series
which can be written in the more compact sigma notation as
- Convergence: A function whose Taylor series converges to the function is called analytic. But sometimes, as we have seen with power series generally, convergence can be local (i.e. only in some interval).